Decisions on partial information
One might have noted that in the examples of the cyclic dependencies with one exclusive resolution, there is always at least one order within the cycle that can be adjudicated without the resolution of the other orders.
For instance, in figure 9 Germany orders its fleet in the North Sea to Norway and gives it support from Skagerrak. This move will succeed, regardless of whether the Russian fleet in Norway succeeds in its move or not. Similarly, in figure 10, the support of Sweden will never be cut, because the convoy will always be disrupted. The success of the Denmark move is irrelevant for the failure of the convoy. It appears then, that in case of a cyclic dependency there is always at least one order in the situation that can be resolved independently.
This principle can be handled more formally. Referring again to figure 9, even without resolving the move of the Russian fleet in Norway, the hold strength of the Norway area might be 0, and will not exceed 1 in any event. The successful support from the fleet in Skagerrak makes the attack strength of the fleet in the North Sea at least 2. So, although we do not know the hold strength precisely, we do know that the attack strength of 2, will always beat it.
This kind of reasoning can be put in an algorithm. To begin, just as for the simple recursive algorithm, we have a UNRESOLVED state for each order, and all orders start in that state. For all the strength values (hold strength, attack strength, defend strength and, prevent strength), we write code that calculates the minimum value and maximum value of the strength given the current state of the orders. In figure 9, the hold strength of the Norway area has a minimum of 0 and a maximum of 1 while the order of the Russian fleet is still UNRESOLVED. If the support of the fleet in Skagerrak is still UNRESOLVED, then the attack strength of the fleet in the North Sea has a minimum of 1 and a maximum of 2. After resolving the support, the minimum also becomes 2.
A move order will get the SUCCEEDS state if the minimum attack strength of the unit beats the maximum resisting strengths of any opposing units. For getting the FAILS state, the maximum attack strength of the unit should not exceed the minimum strengths of the opposing units. If the success or failure of an order still cannot be determined given the information, then the order remains UNRESOLVED. All the equations can be worked out this way.
With this principle, the algorithm remains quite simple. Just start at the top of the order list, and try to resolve each order. Some orders might be resolved right away, while others may stay unresolved. When we are at the bottom of the list, and there are still orders unresolved, we just start a second pass and continue to do so until all orders are resolved. When there are still orders remaining to be resolved, but a pass does not resolve any of them, then there is circular movement or a convoy paradox. The situation (which may consist of multiple independent circular movements or convoy paradoxes) must be passed to a backup rule.
Suppose the algorithm runs on the situation of figure 9:
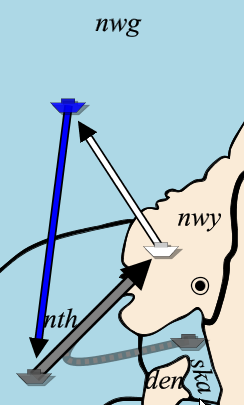 |
England: F nwg -> nth Germany: F ska Supports F nth -> nwy F nth -> nwy Russia: F nwy -> nwg |
If we start at the top, then the order for the English fleet will fail to resolve (the hold strength of the North Sea is 0 or 1). The second order, the support from Skagerrak, will positively resolve. So, does the third order, but the Russian order will remain unresolved.
In the second pass, we know that the hold strength of the North Sea is at least 0 and at most 0. From this information, the fleet in the Norwegian Sea can advance. Finally, at the bottom of the list, the Russian order will be resolved too.
The algorithm can be optimized by resolving any dependency on other orders directly in recursion. Some code must be added to the recursive function to prevent an endless loop in case of cyclic dependency. If the function fails to resolve the order, that additional code can also be used to determine the orders which make up the cyclic dependency.
The principles of this algorithm are used in the adjudicators of Palmpolitik, jDip and Stabbeurfou. Together with the test cases of the DATC, they make it possible to create a high quality adjudicator on the first release (although a truly flawless adjudicator on first release is still a challenge). phpDiplomacy too switched to such an algorithm after its initial release.
Although the algorithm looks good and has proven its usefulness in real programs, two questions remain. First of all, is the algorithm indeed flawless? I assumed that decisions based on partial information can always find the single resolution in case of a cyclic dependency with a single resolution. The examples are evidence that this is indeed the case, but they are not a conclusive proof. In the next chapter I will give this proof.
The second question is whether this is the simplest algorithm. Decisions based on partial information require that each equation be programmed twice. For each strength value we must write code that calculates the minimum, and code that calculates the maximum. For the other equations, it should be realized that if a result is not positive, it is not necessarily negative, because the situation may remain unresolved. This means that separate code must be written to resolve a situation into a positive conclusion, and into a negative conclusion. In the final chapter I will show that there is an alternative, without this double coding.
 |
Lucas Kruijswijk (L.B.Kruijswijk@inter.nl.net) |